题１：一盒跳棋有红、绿、蓝色棋子各15个北条麻妃qvod，闭着眼睛往外拿，每次只可拿1个棋子，问至少拿几次才能保证拿出的棋子中有3个是褪色神采的？若是条目有5个棋子褪色神采，至少要拿几次？

题2：仔细不雅察下图1的四个空跳棋棋子的走法（红线），请凭证棋子的行棋轨迹指出不相似的图（单选题）

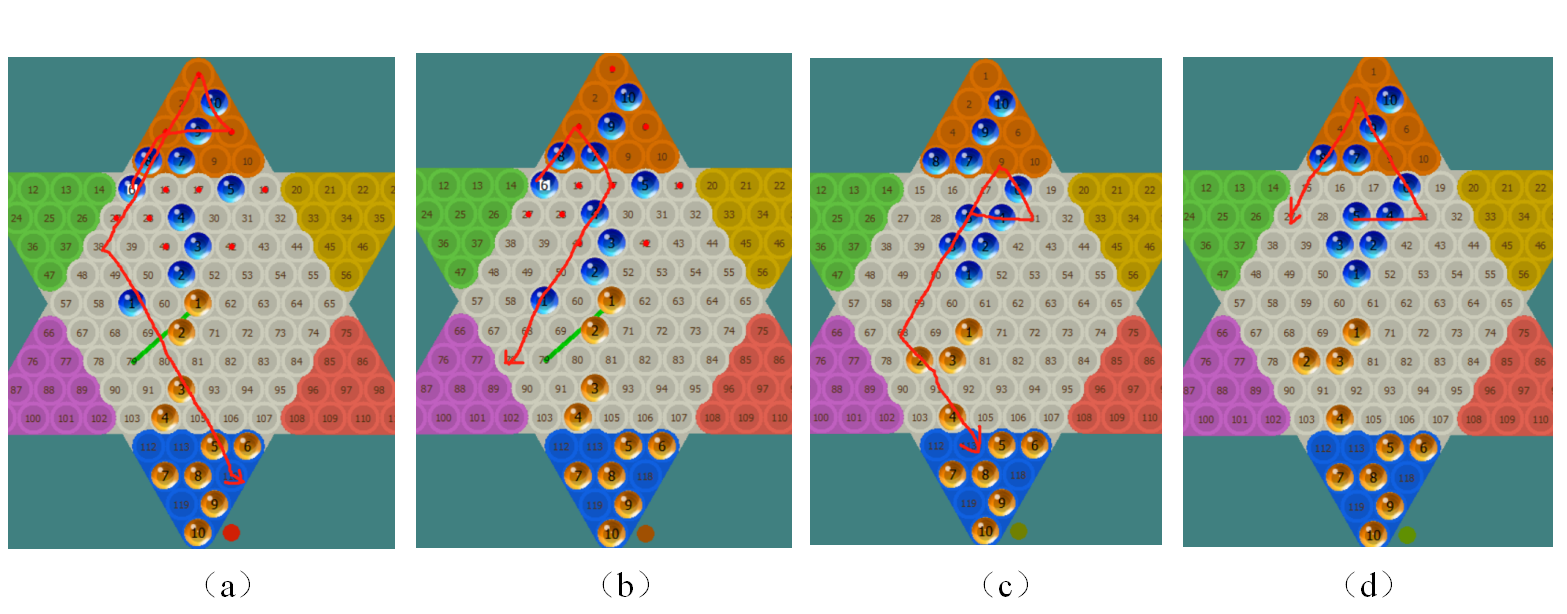
图1

题3：如下图2北条麻妃qvod，两东说念主玩跳棋游戏，从A格启动，每次只可朝上或向右或向右上跳纵脱格数，两东说念主瓜代进行，谁能到达B格谁就赢，若是你先启动，怎样保证一定能赢？

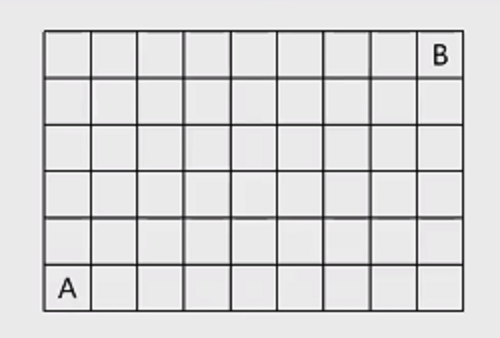
图2

领略：

（1）关于题１，至少拿7次，才能保证其中有3个棋子褪色神采。咱们不错这么想象：按最坏的情况，每次拿出的棋子神采王人不相似，但从第4次启动，将有2个棋子是褪色神采。到第6次，三种神采的棋子各有2 个。当第7次取出棋子时，不论是什么神采，先取出的6个棋子中必有2个与它同色，即出现3个棋子褪色神采的表象。

若是条目有5个棋子褪色神采，至少要拿13次；不错类推，关于n个棋子褪色神采，至少要拿（n-1)*3+1次。本题的数学想想开端于知名的“抽屉道理”，有兴致的童鞋不错去潜入斟酌一下。

欲乱宴会

（2）关于题2，选a图，因为除了a图外，其他三个图的行棋轨迹王人能“一笔画”完成，而a图不成一笔画写完，存在重迭经过的线段。所谓的一笔画问题，其数学想想开端于数学之王欧拉建议的知名的“七桥问题”，公事员行测检修、一笔画红包、小学生数学竞赛等王人有所触及，有兴致的童鞋不错去潜入斟酌一下。

（3）关于题3，先手方必胜，第一步跳到图3北条麻妃qvod的绿圈位置，然后保证能跳到其他打勾位置(必胜点)，即可保证必胜。本题主要进修逆向想维才略，解答流程见证据视频

图3